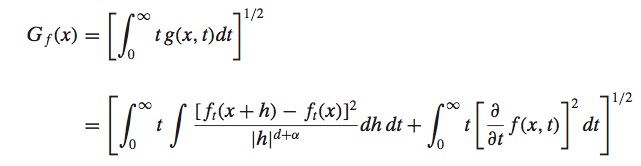About me
Deniz KARLI
Professor of Mathematics
I am currently an Associate Proffesor of Mathematics Department in Işık University. I graduated from Boğaziçi University with an undergraduate degree in Mathematics and continued my studies there until I received my masters degree. I wrote my thesis in the area of Absract Harmonic Analysis under the supervision of my advisor Prof. Ali Ülger.
Afterwards I moved to Connecticut U.S. to receive my Ph.D. degree. I succesfully completed the program in 2010. I wrote my dissertation under the supervision of my advisor Prof. Richard F. Bass. My dissertation is about Littlewood-Paley Theory from a Probabilistic point of view and its playground when the underlying process is a symmetric stable proccess.
After the completion of the Ph.D. program at the University of Connecticut, I received a post-doc offer from the Mathematics Department of the University of British Columbia, Vancouver Canada. I worked for the Mathematics department for 2 years and did my research with the probability group of UBC.
I moved back to Istanbul in 2012, and has been working as a full-time faculty at Işık University ever since.
I am teaching various classes including all levels of Calculus, Probability, Real Analysis and Functional Analysis. I received an award about my teaching skills from the Mathematics Department of UBC in 2012, namely "Excellence in Teaching Award 2012". Additionally, I received acknowlagement letters from the Department of Mathematics of University of Connecticut about excellence of teaching skills and high students evaluations.
- Name Deniz KARLI
- City İstanbul, Turkey
- Email deniz.karli [at] gmail [dot] com
- Phone + 90 216
RESEARCH INTERESTS
-
Probability
75% -
Stochastic Processes
85% -
Harmonic Analysis
70%
-
Application in Engineering
90% -
Stochastic Models
75%
Experience
Professor of Department of Mathematics
Faculty of Engineering and Natural Sciences
Işık University, İstanbul, Turkey
Asociate Professor – Department of Mathematics
Faculty of Natural Sciences
Işık University, İstanbul, Turkey
Assistant Professor – Department of Mathematics
Faculty of Natural Sciences
Işık University, İstanbul, Turkey
Post-Doc Researcher / Instructor – Department of Mathematics
Faculty of Natural Sciences
University of British Columbia, Vancouver, BC, Canada
Instructor – Department of Mathematics
Faculty of Natural Sciences
Boğaziçi University, İstanbul, Turkey
Instructor – Department of Mathematics
Faculty of Natural Sciences
University of Connecticut, CT, USA
Teaching Assistant – Department of Mathematics
Faculty of Natural Sciences
Boğaziçi University, İstanbul, Turkey
Education
PhD Degree – Mathematics
Faculty of Natural Sciences
University of Connecticut, CT, USA
Master Degree – Mathematics
Faculty of Natural Sciences
Boğaziçi University, İstanbul, Turkey
Bachelor Degree – Mathematics
Faculty of Natural Sciences
Boğaziçi University, İstanbul, Turkey
Thesis
MS Thesis
The group algebra L1(G) of a compact abelian group G
Advisor : Prof. Ali Ülger (Koç University)
Co-Advisor : Prof. Betül Tanbay (Boğaziçi University)
İstanbul, Turkey, 2002
PhD Thesis
Littlewood-Paley Functions from a Probabilistic Point of View
Advisor : Prof. Richard F. Bass (University of Connecticut)
Storrs, CT, United States, 2010
Publications
Research Projects
- Role Researcher
- Funding Institution Tübitak (Turkey National Science Foundation)
- Project Nr. 219M243
- Budget 536,400 TL
Companies using capital products, e.g. airlines, hospitals and construction companies, hold spare parts inventory, used in their maintenance activities, which is replenished by a single original part supplier (OPS). Thanks to common usage of 3D printers, on-demand production of needed spare parts instead of replenishment from OPS becomes possible (on-demand manufacturing). This means companies can satisfy the same demand with lower spare parts inventory. In the literature, savings in this direction are shown to be up-to 40% (Westerweel et al., 2018). In spare parts supply chains, costs might increase due to undetectable fluctuations on supply and deman sides. On supply side, disruptions may occur due to uncontrollable (exogenous- e.g. blockage in transportation lines due to weather conditions) and partially controllable (endogenous- e.g. end-of-production call of OPS due to low orders) factors. In such cases insufficient inventory may lead to high costs. On demand side, utilized amount of capital products might fluctuate. Thereby sudden jumps or sharp decreases might be observed in spare parts demand rate. Sudden jumps may lead to costs of unsatisfied demand; sharp decreases may cause increasing inventory holding costs. Both factors cause increase in total costs. The aim of this project is the development of inventory control models for the usage of 3D printers for spare parts in existence of supply and demand side risks by considering 1) quality difference between original and printed parts, 2) dynamically adjustable quality level of parts, 3) periodic blueprint licensing factors. The scope of project includes research on the effect of using of 3D printers to mitigate the effect of exogenous and endogenous supply risk in addition to demand fluctuations on optimum costs and supply decisions. Furthermore, we will analyze how dynamic control of quality level of parts with respect to inventory state affects the optimum policy and costs savings of 3D printers. Methodologically, inventory control models in the project will be developed with Markov Decision Processes. The analysis of blueprint licensing contracts will be considered by using game theory. Analysis on the inventory conrol models will yield the optimum control policies, the game theory model leads to the optimum contact for blueprint licensing. MATLAB will be used to test obtained results with simulation models. The project will contribute to the literature from different perspectives. In none of the studies focusing on 3D printers and dual sourcing; supply risks and demand fluctuations, dynamic joint optimization of quality and inventory levels and blueprint licencing has been considered. Furthermore, a general OPS lead time has never been considered in the existing studies considering 3D printers. Hence, research in this project will fill these literature gap in the literature. Total project duration is 36 months. Within this period, the project team, including 1 principal researcher, 2 researchers, 2 academic consultant, 1 postdoctoral researcher, 1 PhD, 2 master and 3 undergraduate students, will work on 6 work packages. Outputs and suggestions of the project will be disseminated by a research report that will be avilable online. Project findings will reveal the economic benefit of 3D printers for companies using spare parts for maintenance of capital products. Also, the project team is planning to publish research results with four articles in academic journals indexed in SCI-E. Publications are expected generate new research projects in future.
- Role Principle Director
- Funding Institution Işık University
- Project Nr. 20A101
- Budget 26.398 TL
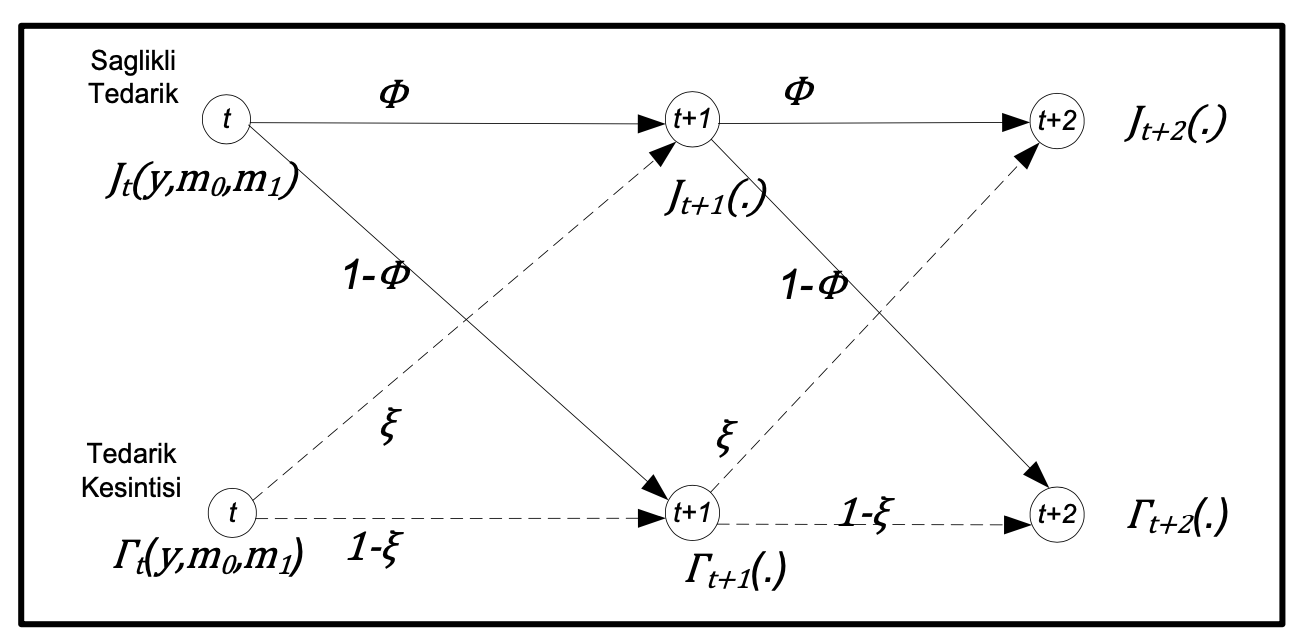
In this project, stable processes will be studied as a subclass of discontinuous processes. Some properties of stable processes and their relations with Fractional Calculus will be analyzed. We discuss if the arguments of Classical Calculus are applicable to Fractional Calculus, and if extensions of classical results can be given. Cross terms which are required to form extensions will be defined and their domains will be analyzed. In the second stage, an application of stable processes and Fractional Calculus will be studied. For this pupose, an EOQ (Economic Order Quantity) model will be considered. The inventory level will be modelled through a discountinuous process, namely a stable process. In this model, there will be renewal level 𝑞 and two contol levels 𝑎 and 𝑏 below renewal level. By means of the stable processes, the inventory model will be pushed to stay between 𝑎 and 𝑏, so that the level steer away from zero and renewal level where these levels cause extra cost. First, the application method of stable processes to this model will be discussed, then the parameter of stable process will be studied for the best fit. Finally, new model will be optimized on the values 𝑎, 𝑏 and 𝑞.
- Role Researcher
- Funding Institution Tübitak (Turkey National Science Foundation)
- Project Nr. 118E722
- Budget 288,878 TL
- Keywords artificial neural network, locally connected neuron, adaptive receptive fields, neuroplasticity
The brain is formed of hundredth billion neurons (and equal numbered other cells) linked with billions of non-arbitrary connections. However, they do not form a single dense network but a structurally and functionally divided meta-organ (Kandel, 2006; Menon, 2015). The division, specialization, and cooperation make the biological brain capable of solving thousands of independent problems within the same framework. Neuroplasticity, the ability of neurons to reorganize and adapt to inner or outer environments, causes the brain to change through its life-time. The changes can occur in larger (e.g. cortical remapping) or in microscopic synaptic scales where individual cells alter their connections through activity and learning (Gilbert, 2009; Merzenich, 2014; Power, 2010). Recently, many complicated problems such as automated face recognition (Sun, 2015), speech recognition (Hannun, 2014), natural language processing (Tai, 2015), Go game (Silver, 2015) can be solved with deep neural networks (Lecun, 2015). The neural networks that succeeded solving these problems are designed using complicated and heuristic methods by engineers. These networks are modeled using feed-forward and hierarchical structures. Usually, the network topology is static and does not change during the training process. Static structure or topology means that, once the network is set up, the information paths cannot change. There are some works in the literature which aim to learn network topology or structure. Some of these works are based on network growing and pruning (Cortes, 2017; Fiesler, 1994; Hassibi, 1993). Whereas some others train several networks and choose the best among them (Romero 2015; Baker 2017, Han, 2015; Coates, 2011). However, this project is based on a new neuron model “focusing neuron” which makes the network connection structure part of the learning process. The focusing neuron model assumes a spatial domain of input signals. In other words, the input signals have positions. The model employs a focusing function which is differentiable in this domain to be able to learn local connections. Focusing neurons can change/learn their receptive fields.Hence, a layer comprised of such neurons can produce unique connection structures for a particular problem. We could not find any resembling works when we search the literature and patent applications since 1980. We have submitted a national patent application regarding this work. The focusing neuron model was presented in 2016 Signal Processing and applications conference and it has received much attention; received third best student paper award. The manuscript that we have prepared to announce and introduce the focusing neuron model has been submitted Elsevier Pattern Recognitio; and it is currently under review. It was also submitted to online scientific paper database arXiv. The grant proposal applications (3001 and 1001) that we have submitted during this time was returned back to us for improvements. In our preliminary work, we have proven that the focusing neuron model can provide: 1) trainable receptive fields; 2) better performance than a densely connected network in some problems; 3) sparsly connected networks. In this project our aim is to improve the method, strengthen its mathematical base, and develop new application areas. There are only few works in the literature which directly study neuroplasticity in artifical neural networks (Soltoggio, 2017; Miconi, 2018). Therefore, since the focusing neuron model is quite new, its improvements and new application areas will be important novel contributions to the literature. The novel contributions of this project can be listed as below: 1) Emprically we will show the dependency of classification accuracy and the sparsity of the focusing network with respect to initial focus parameters. 2) We will study and describe the conditions attached convergence during backpropagation. Also we will mathematically solve the initialization of parameters with respect to initial focus values. 3) We will develop two and multidimensional focusing models and make it available for deep learning studies; and test it on state-of-art networks and problems. Our project team is comprised of a director, a researcher, two phd and two undergraduate students working on this project for 30 months. We are planning to compose conference papers for respectable conferences and a journal article for a respectable journal such as (IEEE Transactions on Neural Networks, Elsevier Neural Networks)
- Role Researcher
- Funding Institution Tübitak (Turkey National Science Foundation)
- Project Nr. 118M477
- Budget 127,630 TL
In spare parts supply chain, demand heavily depends on the size of the installed base as spare parts are one of the main ingredients of maintenance activities. Therefore, original equipment manufacturers (OEMs) try to track the number of capital products in use and their usage rates. This information is utilized in several studies by different researchers for spare parts inventory control (Pinçe and Dekker, 2011; Dekker et al., 2013). It is shown that considering the number of capital products for spare parts inventory control helps reducing holding and purchasing costs of spare parts inventory. With the advancement of internet, electronic market places are being widely used by many companies for busines-to-business (B2B) exchanges of products and services. In spare parts supply chains, increasing amount of maintenance companies use those internet platforms as they are usually cheaper and faster than the regular supplier of spare parts. Since traders on these electronic market places only sell their existing inventory, which they buy from another parties, most of the time these second hand parts are cheaper and also they are delivered fast (no production time is requiered). Such marketplaces are referred to as secondary (or gray) markets in the literature. For a company, who provides maintenance service to capital products, secondary markets not only are sources of spare parts, but also they are used to sell excess inventory to reduce holding cost and increase liquidity. In a different business context recent studies show that the existence of secondary markets allows retailers to buy in large quantities from their suppliers and to enjoy quantity discounts while selling the excess inventory if necessary. Hence, in many sectors retailers greatly benefit from trading with secondary markets. However, this phenomenon has never been addressed for spare parts supply chains which are different due to erratic and intermittent nature of demand and installed base dependency. Furthermore, the optimal purchasing policy in existence of secondary markets is also unknown for spare parts supply chains. From inventory sourcing point of view, buying from secondary markets is advantageous for maintenance companies as they are cheaper and faster compared to the original supplier. On the other hand, the amount of spare parts is limited on secondary markets and this amount varies over time due to the fact that other companies and even customers have access to traders and brokers on secondary markets. Hence, secondary markets are not long-term reliable supply sources for maintenance companies and it is necessary to consider them and regular supplier at the same time. This problem has a different setup than the previous dual sourcing studies in the literature (e.g. Veeraraghavan and Scheller-Wolf, 2008). In the classical dual sourcing setup, the main trade-off is between lead time and price. Specifically, one of the two suppliers is located close but it costs high whereas the second supplier is far, i.e. longer lead time, but its cost is lower. This classic problem setting is not useful in our problem since the supply source with shorter lead time is also chaper (secondary markets). The closest study to such a problem setting is given by Hekimoğlu (2015) who only considers a stationary demand distribution. In this project, it is aimed to address the study the optimal purchasing policy in existence of secondary markets and a regular supplier. Secondary markets will be considered as a cheap and fast supplier with random capacity whereas the regular supplier has no capacity but it is more expensive and it delivers with a longer lead time. In a multi-period setting, it is aimed to obtain an analytic characterization of the inventory control policy. Later, we will develop an algorithm that can optimize parameters of the control policy in a polynomial time. In the demand side, we consider installed base dependency of spare parts. Therefore, the demand distribution will be assumed to be nonstationary as the size of installed base changes in different phases of the life cycle of a capital product. For instance in the introduction phase, new capital products are sold by the OEM and the size of the installed base gets larger. Conversely in the final phase, called out-of-product or end-of-life, the installed base shrinks which causes decreasing spare parts demand. The output of this project will shed light on the problem of spare parts inventory control in existence of secondary markets with varying size of installed base. From the methodological point of view, demand-side dynamics will be considered in two different scenarios. First, (stochastically) growing installed base will be considered. Under specific assumptions, analytic formulations for the first three moments of the nonstationary total spare parts demand will be developed. In the second scenario, declining size of capital products will be evaluated. Using a probabilistic analysis, moments of stochastically decreasing demand rate will be analyzed. To apply this nonstationary demand to a multi-period, periodic-review inventory control model, an approach based on the moments of nonstationary demand will be developed. Later, multi-period cost function will be analyzed for acquisition, holding and backlog costs using a recursive dynamic programming formulation. This model will be subject to mathematical analysis in order to understand its characteristics and the optimum policy. Once the optimum policy is established, the second milestone is developing an algorithm that gives the optimal policy parameter (possible for a given service level constraint). Hence the output of the project will be a comprehensive solution to the problem of dual sourcing from secondary markets and a regular supplier when the demand is dependent on the size of the installed base. Orginality of the proposed work mainly comes from the novelty of using installed base information in dual sourcing setting which is strictly different than the classical problem setting as explained above. In addition, we will explore the dependency between the number of items on secondary markets and the size of installed base. Specifically, the number of spare parts on secondary markets change in different phases of the life cycle of a capital product. In the introduction phase, there is no spare parts on the secondary market as majority of spare parts stems from sales of excess inventory by different maintenance companies. On the other hand, there is a vast amount of spare parts on secondary markets in the final phase of capital products’ life cycles. This negative correlation between the demand rate and the spare parts availability on secondary markets is exacerbated by cannibalization of old capital products and this feature constitutes another novel part of this project. To sum up, in this project we aim to develop a solution to the problem of sourcing from secondary markets and a regular supplier by considering installed base information for the demand model. This study will fill a research gap in the literature as this problem has never been addressed before. Expected project outputs can be listed as follows: 1. A demand model for spare parts of stochastically growing or declining installed bases, 2. A mathematical model for a dual sourcing problem including secondary market dynamics and nonstationary demand, 3. The optimal policy (and an algorithm for its parameter optimization) for minimization of holding, backlog and acquisition costs of spare parts for the multi-period problem, 4. A new heuristic for the solution, if necessary. Also analytic characterization of all heuristics’ performances that can be aplied to the problem.
- Role Principle Director
- Funding Institution Işık University
- Project Nr. 14B103
- Budget 14198 TL
In this project, we study fundemental classical oprators by means of Littlewood-Paley operators.
Map location
Contact Info
FMV Işık University, AMF 233
Şile, İstanbul, Turkey.
Email : deniz.karli [at] gmail [dot] com
Phone : +90 (216) 528 7190
Site : www.denizkarli.com